Что открыл эратосфен

Эратосфен и география

Ученый был первым, кто дал географии ее имя, которое означает, что география изучает не только обитаемые области, но всю Землю.

• В работе «География», состоящей из 3-х книг, ученый представил научный обзор всех греческих достижений, обосновал «математическую» географию, высказал взгляд на Землю, как шарообразное тело, привел данные о поверхности. Ученый попытался оценить расстояния до Солнца и Луны и их размеры. В работе описаны затмения Солнца и Луны, высказано предположение о длительности дня на разной широте.
• Его главное открытие – размер земного шара, вычисленный геометрически. Для этого он предпринял путешествие из Александрии в Сиену (современный Асуан).

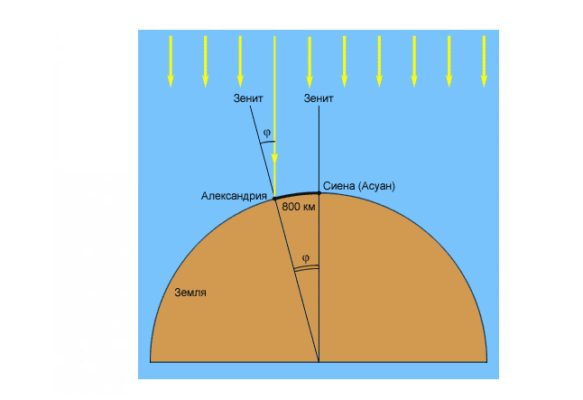Рис. 1. Измерение и расчет Эратосфеном радиуса Земли.

Длина экватора, вычисленная Эратосфеном отличается от полученной современными методами всего на 385 км; это было самое точное определение того времени.

Не менее важное определение – угол наклона земной оси, сделанное не менее точно.
Предложена идея плавания к Индии, которая подтолкнула путешественника Колумба к разработке маршрута через Атлантику. Приложением к «Географии» была карта мира, созданная ученым

На карте впервые появились параллели и меридианы.

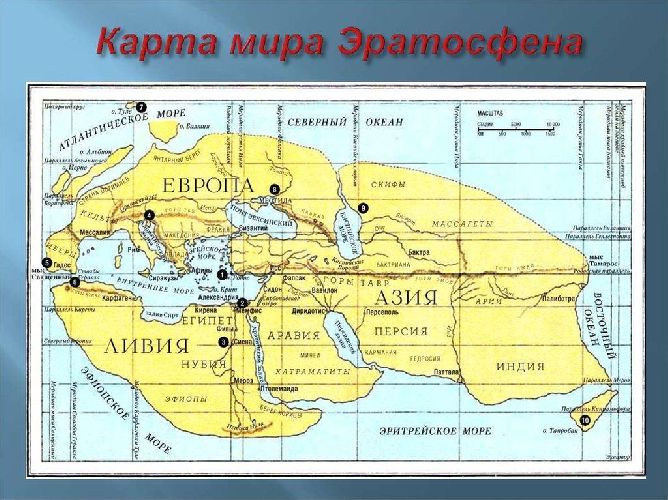Рис. 2. Карта Эратосфена.

Что открыл Эратосфен в географии

Для своих размышлений и заключений древнегреческий философ употребил термин «география» (дословно: «землеописание»). Накопленный опыт и всесторонняя начитанность помогли ему составить общую картину земной поверхности.

Он высказал предположения о световом дне, его изменениях и отличиях в разных точках мира. Эратосфен измерил земной шар посредством деления участков на сектора. Его метод впоследствии преобразовался в концепцию параллелей и меридианов.

В своих исследованиях эллин пришел к выводу: если добраться до Гибралтара, а после плыть строго на запад, море приведет к берегам Индии. 

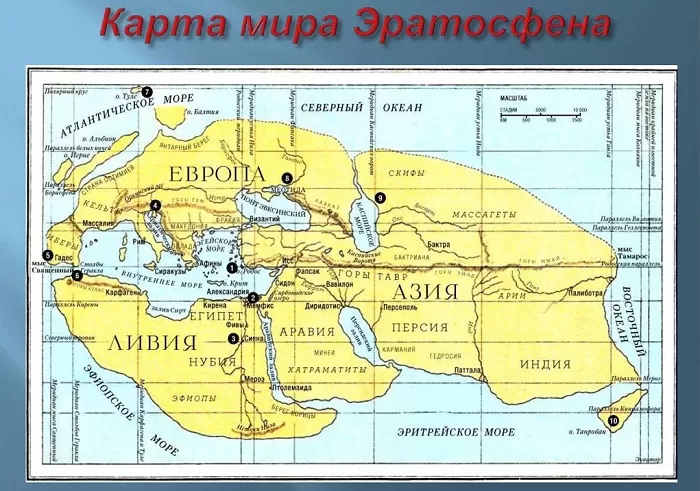
По итогам научных трудов Эратосфеном была составлена карта мира. И пусть она не совсем похожа на современные высокоточные фото Земли, для античного времени это было значительное открытие.

Отец географии установил точное положение крупных городов своего времени, островов и материков относительно друг друга, рассчитал их примерное положение на поверхности планеты.

https://youtube.com/watch?v=iIFCfs1f-Cg

Описание алгоритма

Наша цель — посчитать для каждого числа от в отрезке его минимальный простой делитель .

Кроме того, нам потребуется хранить список всех найденных простых чисел — назовём его массивом .

Изначально все величины заполним нулями, что означает, что мы пока предполагаем все числа простыми. В ходе работы алгоритма этот массив будет постепенно заполняться.

Будем теперь перебирать текущее число от до . У нас может быть два случая:

— это означает, что число — простое, т.к. для него так и не обнаружилось других делителей.

Следовательно, надо присвоить и добавить в конец списка .

— это означает, что текущее число — составное, и его минимальным простым делителем является .

В обоих случаях дальше начинается процесс расстановки значений в массиве : мы будем брать числа, кратные , и обновлять у них значение . Однако наша цель — научиться делать это таким образом, чтобы в итоге у каждого числа значение было бы установлено не более одного раза.

Утверждается, что для этого можно поступить таким образом. Рассмотрим числа вида:

где последовательность — это все простые, не превосходящие (как раз для этого нам понадобилось хранить список всех простых чисел).

У всех чисел такого вида проставим новое значение — очевидно, оно будет равно .

Почему такой алгоритм корректен, и почему он работает за линейное время — см. ниже, пока же приведём его реализацию.

Удивительная история

Древнегреческий мыслитель изучал историю, философию, литературу и множество других дисциплин. Современники посмеивались над ним и считали дилетантом, поскольку, по их мнению, он интересовался всем, но толком не знал ничего. Однако ученого это не смущало. Эратосфен работал в египетской Александрии. Однажды, возвращаясь из своего музея, он повстречал путешественников, идущих из Сиены — города, расположенного южнее Александрии, на Северном тропике (современное название — Асуан). Те поделились с ученым любопытным наблюдением: когда они находились в Сиене (а это был самый длинный день в году), ни один предмет в городе не отбрасывал тень.

Эратосфен не мог оставить сказанное без внимания, поэтому спустя год посетил Сиену и убедился, что путники его не обманули. Он заглянул в глубочайший городской колодец и увидел: солнечные лучи достигают его дна, а также подметил, что светило в данный момент располагалось ровно над головой. В это же время в Александрии оно висело гораздо ниже и абсолютно все предметы, на которые падали лучи, отбрасывали небольшую тень. Такое простое наблюдение натолкнуло Эратосфена на мысль об определении размеров Земли.

Предстваление о Земле древних людей

Сейчас каждому ребенку известно, что Земля имеет шарообразную форму. Но далеко не всегда это было очевидно. Древним людям было очевидно совсем другое: Земля плоская. В замечательной сказке о старике Хоттабыче пионер Волька, заколдованный древним джинном, говорит учительнице: «Если бы Земля была шаром, воды стекли бы с нее вниз, люди умерли бы от жажды, а растения засохли».

Представление древних: мир покоится на трех слонах, стоящих на огромной черепахе

Например, в Древней Индии считали, что Земля покоится на спинах трех слонов, стоящих на спине черепахи, которая плывет по океану. Вавилоняне мыслили Землю огромной горой, поднимающейся из бесконечных вод. Древние евреи считали, что Земля — бесконечная равнина, под которой текут воды, а ветры приносят то дождь, то засуху…

Первые шаги в верном направлении, как и во множестве других наук, сделали эллины — жители Древней Греции.

Родоначальники географии

Эратосфен Киренский (276-194 гг. до н. э.) — древнегреческий математик, астроном и географ, основоположник географии как науки. Первым доказал,что Земля имеет форму шара

В древности каждый путешественник в сущности являлся первооткрывателем. Война, торговля, да и просто извечное человеческое любопытство побуждали минойцев, финикийцев и многие другие народы пускаться в опаснейшие плавания по морю или походы по суше. Две тысячи лет назад египтяне исследовали центральные области Африки, побережья Средиземного и Красного морей. Чуть менее тысячи лет назад в Древнем Китае перед постройкой крепости составлялись подробные карты местности, а в III веке до нашей эры китайцам уже был известен компас.

История сохранила для нас некоторые имена: Арриан, Страбон, Анаксимандр… Многие древнегреческие ученые внесли большой вклад в развитие географии. Но ее истинным родоначальником принято считать Эратосфена Киренского, который не только предположил, что Земля шарообразна, но и доказал это, применяя математические вычисления.

Географы древности:

• Гекатей (546480 гг. до н. э.) — составил «Землеописание» на основе береговых лоций
• Геродот (485425 гг. до н. э.) — путешествовал от Дона до порогов Нила. Путевые заметки легли в основу его знаменитой «Истории»
• Аристотель (384-322 гг. до н. э.) — основатель гидрологии, метеорологии и океанологии

Поиски длины экватора

Одной из задач, которая в особенности интересовала древнегреческого мастера географии, был вопрос поиска длины окружности Земли. За основу своей теории, приведшей к удивительным для того времени результатам, исследователь взял то, что города Александрия и Сиена (ныне Асуан) расположены на одном и том же меридиане. Киренский ученый наблюдал за отношением угла падения лучей, отбрасываемых небесным светилом в день летнего солнцестояния в двух этих населенных пунктах, к поверхности земли.

В своем исследовании математик и географ пользовался гномоном — специальным устройством, изобретенным другим древнегреческим ученым Анаксимандром Милетским и позволяющим с высокой точностью определить момент астрономического полдня.

Многолетние наблюдения за светом и тенью позволили Эратосфену вычислить необходимый угол падения солнечных лучей. На основании полученных данных и произведенных с ними расчетов он высказал предположение, что фактическое расстоянием между Александрией и Сиеной равняется 785 км.

Соотнеся полученное расстояние и значение угла 1 к 50, определенное при помощи гномона, древний математик и географ смог совершить прорыв, узнав примерную длину экватора Земли, которая, согласно его подсчетам, составила около 39250 км. Согласно современным высокоточным измерениям, длина экватора равняется 40120 км.

Это великое открытие не только перевернуло античную географию, но и позволило Эратосфену прославиться за пределами своего места нахождения. Благодаря полученным данным ученый смог вычислить радиус земного шара, довольно точно определить фактическое расстояние между населенными пунктами в пределах одного материка и узнать, как далеко находятся Африка и другие континенты. Такой вклад в развитие античных представлений об окружающем мире невозможно не оценить.

География в XVII-XIX века

В 1650 году германо-голландский географ Бернхард Варен(1622-1650/1651) написал книгу «География генеральная», в которой определил цели, задачи и методы географии как научной дисциплины. Этот труд был высоко оценен Петром I и по его приказу переведен на русский язык.

Лазарев Михаил Петрович — русский адмирал, первооткрыватель Антарктиды

Американские ученые изучали свой континент, в Западной Европе выпускали точные и подробные географические энциклопедии, а в России развитие географии шло рука об руку с освоением огромных территорий за Уралом. Огромный вклад в изучение этой области внесли русские ученые М. В. Ломоносов и В. Н. Татищев.

Век XIX стал эпохой бурного технического развития. Такие имена, как Александр фон Гумбольдт, Карл Риттер, Петр Семенов-Тян-Шанский, Николай Миклухо-Маклай, без сомнения, известны практически всем. Ученые объединялись в географические школы и сообщества, впервые делались попытки не просто описать, а объяснить не только отдельные явления, но и их взаимосвязь.

В 1820 году русская экспедиция под руководством Фаддея Беллинсгаузена и Михаила Лазарева открыла последний неизвестный материк — Антарктиду.

Казалось, век географии подходит к концу. Но так ли это было на самом деле?

Эпоха Велики географических открытий

До XV века весь мир пользовался трудами греческих ученых: Страбона (ок. 64 г. до н. э. — ок. 23 г. н. э.) и Клавдия Птолемея (ок. 100 г. н. э. — ок. 170 г. н. э.). Первый создал колоссальный 17-томный труд по географии древнего мира, хранившийся в Александрийской библиотеке. Второй изучал, комментировал и дополнял работы Страбона с точки зрения астрономии, математики и механики.

Компас (от итал. compassare — измерять шагами) — магнитное устройство для определения сторон света. Впервые был подробно описан в китайской книге 1044 г., хотя изобретен раньше

Но XV и XVI века стали временем огромного прорыва. Мир немыслимо расширился, распахнулся во все стороны: были открыты неведомые ранее острова и материки, реки, моря и океаны, новые народы и их культурные традиции, появились первые карты земного шара и первый географический атлас. Примерно тогда же, в конце XVI века, была создана одна из древнейших карт Российского государства — «Большой чертеж».

Это время было названо эпохой Великих географических открытий, и мы поговорим о них в отдельной главе.

Различные оптимизации решета Эратосфена

Самый большой недостаток алгоритма — то, что он «гуляет» по памяти, постоянно выходя за пределы кэш-памяти, из-за чего константа, скрытая в , сравнительно велика.

Кроме того, для достаточно больших узким местом становится объём потребляемой памяти.

Ниже рассмотрены методы, позволяющие как уменьшить число выполняемых операций, так и значительно сократить потребление памяти.

Просеивание простыми до корня

Самый очевидный момент — что для того, чтобы найти все простые до , достаточно выполнить просеивание только простыми, не превосходящими корня из .

Таким образом, изменится внешний цикл алгоритма:

for (int i=2; i*i<=n; ++i)

На асимптотику такая оптимизация не влияет (действительно, повторив приведённое выше доказательство, мы получим оценку , что, по свойствам логарифма, асимптотически есть то же самое), хотя число операций заметно уменьшится.

Решето только по нечётным числам

Поскольку все чётные числа, кроме , — составные, то можно вообще не обрабатывать никак чётные числа, а оперировать только нечётными числами.

Во-первых, это позволит вдвое сократить объём требуемой памяти. Во-вторых, это уменьшит число делаемых алгоритмом операций примерно вдвое.

Уменьшение объёма потребляемой памяти

Заметим, что алгоритм Эратосфена фактически оперирует с битами памяти. Следовательно, можно существенно сэкономить потребление памяти, храня не байт — переменных булевского типа, а бит, т.е. байт памяти.

Однако такой подход — «битовое сжатие» — существенно усложнит оперирование этими битами. Любое чтение или запись бита будут представлять из себя несколько арифметических операций, что в итоге приведёт к замедлению алгоритма.

Таким образом, этот подход оправдан, только если настолько большое, что байт памяти выделить уже нельзя. Сэкономив память (в раз), мы заплатим за это существенным замедлением алгоритма.

В завершение стоит отметить, что в языке C++ уже реализованы контейнеры, автоматически осуществляющие битовое сжатие: vector<bool> и bitset<>. Впрочем, если скорость работы очень важна, то лучше реализовать битовое сжатие вручную, с помощью битовых операций — на сегодняшний день компиляторы всё же не в состоянии генерировать достаточно быстрый код.

Блочное решето

Из оптимизации «просеивание простыми до корня» следует, что нет необходимости хранить всё время весь массив . Для выполнения просеивания достаточно хранить только простые до корня из , т.е. , а остальную часть массива строить поблочно, храня в текущий момент времени только один блок.

Пусть — константа, определяющая размер блока, тогда всего будет блоков, -ый блок () содержит числа в отрезке . Будем обрабатывать блоки по очереди, т.е. для каждого -го блока будем перебирать все простые (от до ) и выполнять ими просеивание только внутри текущего блока. Аккуратно стоит обрабатывать первый блок — во-первых, простые из не должны удалить сами себя, а во-вторых, числа и должны особо помечаться как не простые. При обработке последнего блока также следует не забывать о том, что последнее нужное число не обязательно находится в конце блока.

Приведём реализацию блочного решета. Программа считывает число и находит количество простых от до :

const int SQRT_MAXN = 100000; // корень из максимального значения N
const int S = 10000;
bool nprimeSQRT_MAXN, blS;
int primesSQRT_MAXN, cnt;
 
int main() {
 
	int n;
	cin >> n;
	int nsqrt = (int) sqrt (n + );
	for (int i=2; i<=nsqrt; ++i)
		if (!nprimei) {
			primescnt++ = i;
			if (i * 1ll * i <= nsqrt)
				for (int j=i*i; j<=nsqrt; j+=i)
					nprimej = true;
		}
 
	int result = ;
	for (int k=, maxk=nS; k<=maxk; ++k) {
		memset (bl, , sizeof bl);
		int start = k * S;
		for (int i=; i<cnt; ++i) {
			int start_idx = (start + primesi - 1)  primesi;
			int j = max(start_idx,2) * primesi - start;
			for (; j<S; j+=primesi)
				blj = true;
		}
		if (k == )
			bl = bl1 = true;
		for (int i=; i<S && start+i<=n; ++i)
			if (!bli)
				++result;
	}
	cout << result;
 
}

Асимптотика блочного решета такая же, как и обычного решета Эратосфена (если, конечно, размер блоков не будет совсем маленьким), зато объём используемой памяти сократится до и уменьшится «блуждание» по памяти. Но, с другой стороны, для каждого блока для каждого простого из будет выполняться деление, что будет сильно сказываться при меньших размерах блока. Следовательно, при выборе константы необходимо соблюсти баланс.

Как показывают эксперименты, наилучшая скорость работы достигается, когда имеет значение приблизительно от до .

Улучшение до линейного времени работы

Алгоритм Эратосфена можно преобразовать в другой алгоритм, который уже будет работать за линейное время — см. статью «Решето Эратосфена с линейным временем работы». (Впрочем, этот алгоритм имеет и недостатки.)

Научные труды: математика

Из сочинений, посвященных математическим проблемам, в полном составе до наших дней дошло лишь письмо, обращенное к царю Птолемею, в котором ученый рассказывает об удвоении куба и описывает прибор, вошедший в историю науки под названием мезолябия.

О других математических сочинениях и о том, что открыл Эратосфен в математике, мы можем судить лишь по отрывочным сведениям из сторонних источников, таких как труды Паппа и Евтокия, один из которых ссылается на работы старшего коллеги, а второй и вовсе цитирует Эратосфена.

Есть, однако, одно довольно любопытное сочинение, о котором европейская наука узнала от последователя среднего платонизма Теона Смирнского. В своем сочинении средневековый ученый упоминает работу «Платоник», в которой Эратосфен рассуждает о пропорциях и отношениях равенства.

Стоит отметить, что труды ученого были крайне популярны у последователей платонизма в lll веке нашей эры. Например, Никомах Герасский, известный как математик и теоретик музыки, в своем сочинении «Введение в арифметику» довольно пространно цитирует неизвестное сочинение Эратосфена, используя его имя в качестве неоспоримого авторитета как в математике, так и в гармонии, и поэтике.

Говоря о том, что Эратосфен открыл и в каком году, нельзя не упомянуть так называемое решето Эратосфена, которое представляет собой алгоритм для нахождения простого числа в любом заранее заданном пределе.

Литература[править | править код]

• Античная география. М., 1953.
• Бобынин В. В. Эратосфен // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
• Дитмар А.Б. Родосская параллель: Жизнь и деятельность Эратосфена. — М.: Мысль, 1965. — 72 с.
• Колчинский И.Г., Корсунь А.А., Родригес М.Г. Астрономы: Биографический справочник. — 2-е изд., перераб. и доп. — Киев: Наукова думка, 1986. — 512 с.

На иностранных языках

• Aujac G. Eratosthène de Cyrène, le pionier de la geographie. — Paris: Édition du CTHS, 2001. — 224p.
• Diller A. Geographical Latitudes in Eratosthenes, Hipparchus and Posidonius // Klio. — 1934. — Bd. 27. — Heft 3. — S. 258—269.
• Dutka J. Eratosthenes’ measurement of the Earth reconsidered. Archive for History of Exact Sciences, 46, 1993, p. 55-64.
• Fraser P. M. Ptolemaic Alexandria. — Oxford: Clarendon Press, 1972.
• Goldstein B. R. Eratosthenes on the measurement of the Earth // Historia Mathematica. — Vol. 11. — 1984. — P. 411—416.
• Rawlins D. Eratosthenes’ geodesy unraveled: was there a high-accuracy Hellenistic astronomy, Isis, 73, 1982, p. 259—265.
• Rawlins D. The Eratosthenes — Strabo Nile map. Is it the earliest surviving instance of spherical cartography? Did it supply the 5000 stades arc for Eratosthenes’ experiment?, Arch. Hist. Exact Sci, 26 (3), 1982, p. 211—219.
• Rawlins D. Eratothenes’s large earth and tiny universe. DIO, 14, 2008.
• Shcheglov D. A. Ptolemy’s System of Seven Climata and Eratosthenes’ Geography // Geographia Antiqua. — Vol. 13. — 2004 (2006). — P. 21-37.
• Thalamas A. La géographe d’Ératosthène. — Versailles, 1921.
• Wolfer E. P. Eratosthenes von Kyrene als Mathematiker und Philosoph. — Groningen-Djakarta, 1954.

2. Работы и сочинения Эратосфена

2.1. Работы по математике

Из сочинений Эратосфена по математике до нашего времени дошло только написанное к царю Птолемею письмо об удвоении куба. Это письмо сохранилось в комментарии Евтокия к трактату Архимеда О шаре и цилиндре. В письме содержатся некоторые исторические сведения о делийской задаче, а также описание прибора, изобретённого самим автором и известного под именем мезолябия.

Сведения о других математических сочинениях Эратосфена отличаются крайней неполнотой. Папп в двух местах своего Собрания называет сочинение Эратосфена О средних величинах, замечая при этом, что оно во всех своих предположениях стоит в связи с линейными местами.

О сочинении Эратосфена Платоник, посвящённом пропорциям, говорит Теон Смирнский. Возможно, что именно к Эратосфену восходит алгоритм «разворачивания всех рациональных отношений из отношения равенства», описанный Теоном Смирнским и Никомахом Герасским.

Отрывок из ещё одного сочинения Эратосфена приводит во Введении в арифметику Никомах Герасский. То же делает и Ямвлих в своём комментарии к этому сочинению Никомаха. Предмет этого отрывка состоит в изложении найденного Эратосфеном способа определения произвольного количества последовательных простых чисел (так называемое решето Эратосфена).

2.2. Работы по астрономии

Из сочинений Эратосфена по астрономии до нашего времени дошло только одно, Катастеризмы — перечисление созвездий и заключающихся в них звёзд, числом до 700. Определения положений этих звезд сочинение не даёт.

Для своих астрономических наблюдений Эратосфен установил под портиком здания Мусейона большие армиллярные сферы.

Эратосфен определил угловое расстояние от экватора до тропика: он нашёл его равным 11/83 от 180°.

2.3. Работы по геодезии и географии

В тесной связи с астрономией находится работа Эратосфена, состоящая в измерении длины земного меридиана. Краткое изложение этой работы известно нам по трактату Клеомеда «О круговращении небесного свода»:

Измерение Земли по Эратосфену

Карта Эратосфена

Позднее полученное Эратосфеном число было увеличено до 252000 стадиев. Определить, насколько эти оценки близки к реальности, трудно, поскольку неизвестно, каким именно стадием пользовался Эратосфен. Но если предположить что речь идёт о греческом (178 метров), то его радиус земли равнялся 7,082 км, если египетским, то 6,287 км. Современные измерения дают для усреднённого радиуса Земли величину 6,371 км. Что делает выше описанный расчёт выдающимся достижением и первым достаточно точным расчётом размеров нашей планеты.

В сравнительно больших отрывках дошло до настоящего времени сочинение Эратосфена о географии. В полном своём составе оно делилось, по свидетельству Страбона, на три книги. В первой автор дал критический обзор истории географии, от первого появления географических понятий у Гомера до своих непосредственных предшественников, то есть до историков и географов, воспользовавшихся походами Александра Македонского и их описаниями. Вторая книга излагает основы географии по взглядам самого автора. Предмет третьей книги составляет суша.

2.4. Другие работы Эратосфена

Эратосфен является основателем научной хронологии. В своих Хронографиях он пытался установить даты, связанные с историей Эллады, составил список победителей Олимпийских игр.

Сохранились отрывки из сочинения Эратосфена О древней комедии и из двух его поэм; в одной он вкладывает в уста Гермеса рассказ о строении неба, светил и гармонии сфер, в другой передаётся легенда об Эригоне, дочери Икара.

биография

Первые годы

Эратосфен родился примерно в 276 г. до н.э. в Кирене, греческом городе, расположенном в Северной Африке, на территории, которая сейчас является территорией Ливии

Он был сыном Аглауса, о котором не ведется никаких исторических записей, поэтому считается, что он не был из важной семьи в то время

Несмотря на то, что Эратосфен не имел выдающегося происхождения, он приехал из города, который получил признание людей, которые родились в нем. Кирена была основана греками Теры до 600 г. до н.э. и процветала как независимый город до прихода эллинской эры..

Кирена была поглощена Птолемейской монархией Египта, которая управляла Александрией, культурным и торговым центром Средиземноморья. Был большой книжный магазин, музей и школа повышения квалификации.

Эратосфен пошел по стопам других ученых в своем городе и обучался у Лисании, эксперта по грамматике. Несмотря на то, что в греческие времена молодые люди из богатых семей имели больший доступ к образованию, для мужчин существовали академии.

Дети с семи лет обучались таким предметам, как литература, спорт и музыка. Считается, что Эратосфен также мог быть учеником Каллимах.

Афины

Основным интересом Эратосфена к юности была философия, и это призвание привело его в Афины в возрасте 15 лет. Там он оставался примерно 25 лет. Затем он подготовил и приобрел известность как академический.

В Афинах он нашел так много философов, что он был поражен и поражен. Сначала он учился у Зенона в школе стоиков. Также с одним из его учеников, Аристоном де Хиосом, из которого он написал биографию. Но он не нашел в них стиля, который ему нравился.

Затем он присоединился к платоникам как ученик Арцесилао. Именно тогда Эратосфен создал произведение под названием Platonicus, в которой, следуя методу Платона, он исследовал математические и космологические темы. В то время он также написал Пери Агатōн кай какōN, текст, который был потерян.

После этих переживаний он разочаровался в философии и решил посвятить себя поэзии. Так началась слава Эратосфена, так как в своей новой области он добился признания, которого хотел.

Тексты не сохранились от его первых произведений в качестве поэта; однако некоторые имена передавались потомкам в цитатах других греков. Гермес это была одна из его работ, в которой он обратился к жизни бога, а другой взял по имени Эригона.

Александрия

Считается, что именно слава Эратосфена как поэта привлекла внимание Эвергетеса Птолемея III, который призвал его в Александрию, чтобы он занялся репетиторством своего сына, а также предложил ему должность директора городской библиотеки.. Птолемей III был тронут не только интересом к работе Эратосфена, но и политическими соображениями

Город Кирена прошел независимый период Египта до брака между Птоломео III и Беренис, дочерью Магаса, губернатора этого города

Птолемей III был тронут не только интересом к работе Эратосфена, но и политическими соображениями. Город Кирена прошел независимый период Египта до брака между Птоломео III и Беренис, дочерью Магаса, губернатора этого города.

В поисках защиты своего недавно восстановленного домена Птолемей III видел, как хорошо удовлетворить жителей Кирены, предлагая Эратосфену такую ​​же должность, как глава великой Александрийской библиотеки..

В период, когда Эратосфен руководил Александрийской библиотекой, в ней были достигнуты большие успехи. Приобретенные произведения, такие как великие драмы Эсхила и Еврипида. Они также расширили исследования в Софокла.

В эту эпоху Эратосфен воспользовался своим положением и доступом к информации, которую ему пришлось изучать по самым разным предметам. Однако он никогда не хотел специализироваться на одном предмете, поэтому некоторые упрекали его.

смерть

Эратосфен умер в Александрии, около 194 г. до н.э., когда ему было 82 года. Некоторое время назад он ослеп в результате катаракты и, как полагают, совершил самоубийство от голода.

Несмотря на его большой вклад в науку, его работа не была воспроизведена многими другими, по-видимому, потому что у него не было достаточно студентов, чтобы передать свои открытия и теории.

Тем не менее, его вклад в изучение земли дал ему титул отца географии. В течение своей жизни Эратосфен был любителем знаний во всех областях.